En présence de sols contaminés sous bâtiment, le principal risque sanitaire pour les occupants est l’inhalation de Composés Organiques Volatils (COV), présents dans les gaz du sol. Ceux-ci vont migrer, soit par diffusion et/ou advection à travers la zone non saturée (ZNS), vers l’espace intérieur du bâtiment à l’aplomb (Figure 1), par l’intermédiaire des fissures du plancher. L’advection peut avoir lieu car la majorité des bâtiments sont sous une légère dépression vis-à-vis du sol (principalement en raison de la différence de température entre le sol et l’air intérieur).

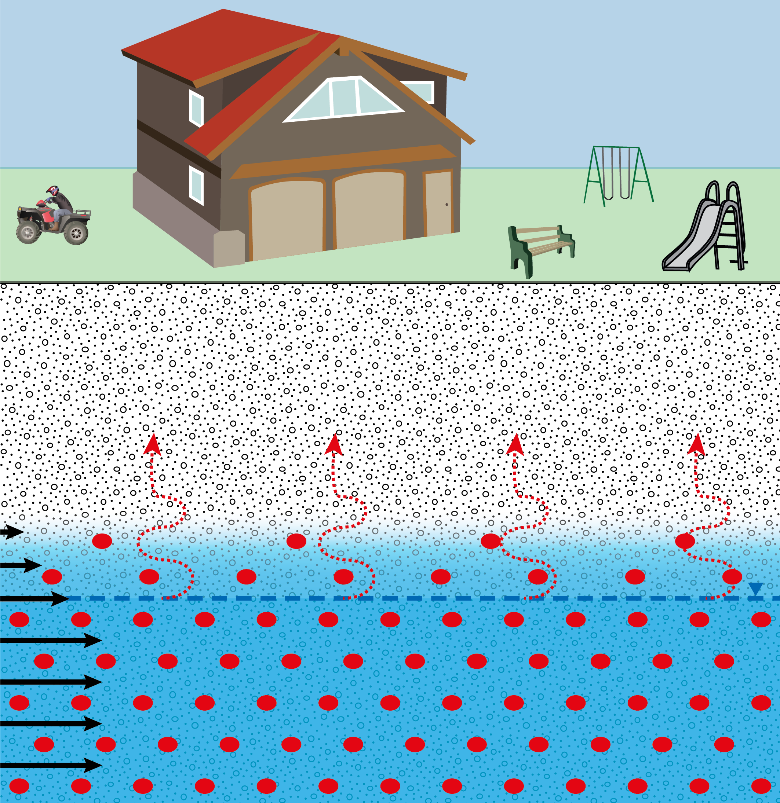
Afin de comparer simplement les flux de contaminants volatils à partir d’une contamination sous forme dissoute pour différents types de sol, InnovaSol a développé un outil simple, mis à disposition sous forme de tableur à télécharger à la fin de cet article.

Les bases théoriques de l’outil

Afin de quantifier le risque associé à une contamination de ce type, il est nécessaire de comprendre les mécanismes de transport régissant la migration de contaminants organiques sous forme gazeuse vers la surface ainsi que les facteurs d’atténuation influant sur cette migration.

Les travaux de Hers et al. (2003) et Fitzpatrick et Fitzgerald (2002) montrent que la ZNS joue un rôle primordial dans l’estimation des flux gazeux de la nappe vers la surface :

• D’une façon générale, le type de polluant change relativement peu les flux tant que celui-ci est volatil.
• La perméabilité équivalente des fondations du bâtiment influence peu les résultats généraux.
• Dans les sols peu perméables à l’air, le processus majeur est la diffusion et ainsi le différentiel de pression entre sol et bâtiment est peu influent.
• A l’inverse, dans les sols perméables, les paramètres majeurs sont la perméabilité à l’air du sol et la différence de pression sol-bâtiment.
• La teneur en gaz du sol, qui peut varier largement sous un bâtiment, influence de façon très conséquente les résultats.

Caractériser la ZNS avec les courbes capillaires d’un sol

Le sol va présenter une porosité et un profil de teneur en eau en fonction de l’altitude spécifique (appelée courbe capillaire). Ces deux paramètres sont principalement liés à la granulométrie du sol. Par exemple, un sable grossier « retiendra moins l’eau » qu’un sol limoneux et les courbes capillaires de la ZNS seront donc différentes. Ainsi, la zone proche de la saturation appelée frange capillaire sera mince dans le cas d’un sable grossier tandis qu’elle pourra atteindre plus d’un mètre dans un sol limoneux. Classiquement, ces courbes capillaires sont décrites par le modèle de Van Genuchten (1980). La Figure 2 montre quelques courbes capillaires pour différents types de sol.

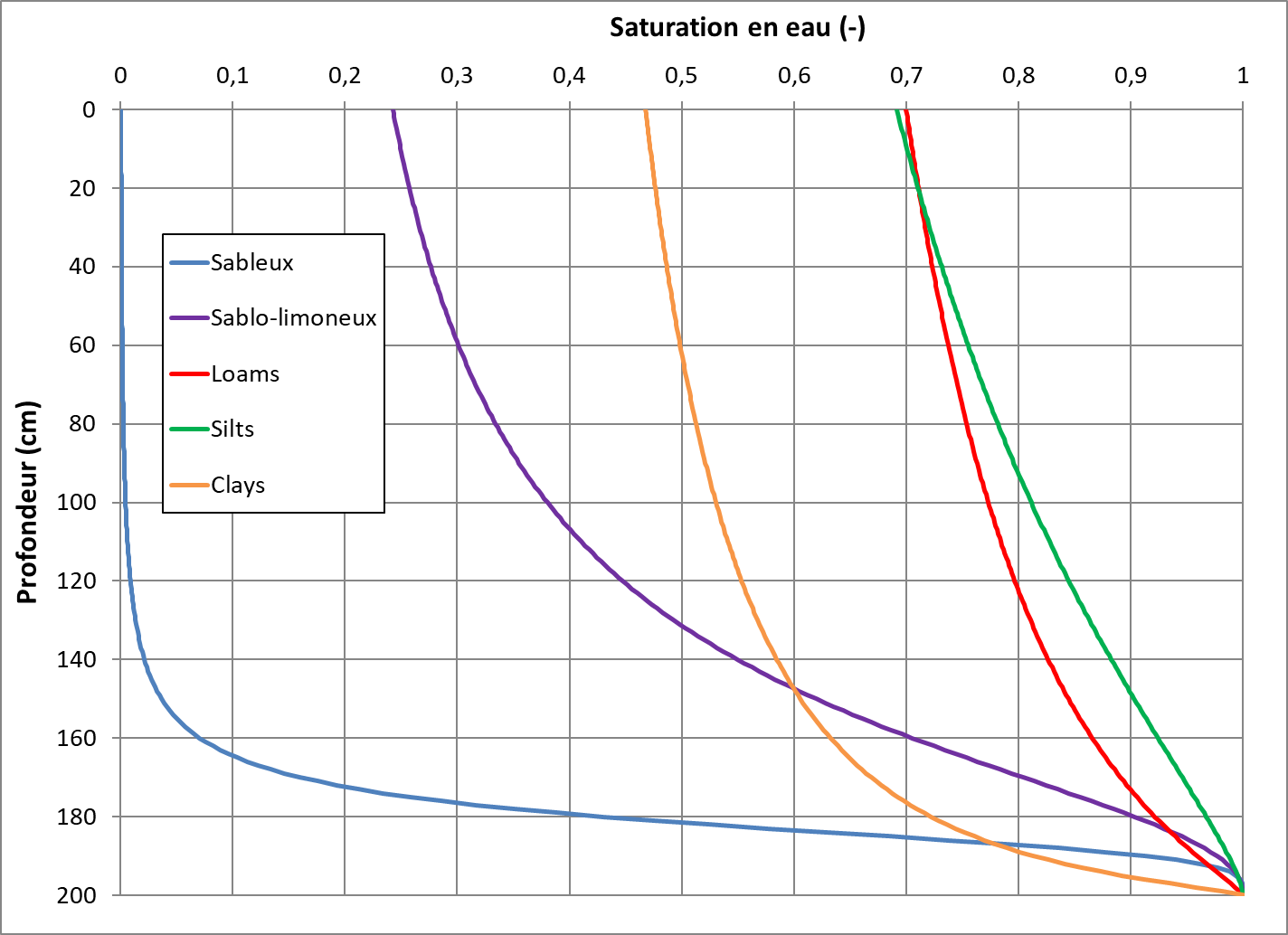
Caractériser la diffusion de gaz dans la ZNS

Sur le long terme, la migration de COV dans la ZNS se fait principalement par diffusion. Pour la caractériser, il faut appliquer la loi de Fick décrivant que le flux J est proportionnel au gradient de concentration et à un coefficient de diffusion effective D_eff :

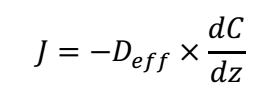
Ce flux est celui qui servira à calculer le risque dans les bâtiments sus-jacents. Dans un sol, le coefficient de diffusion effective est principalement fonction des propriétés du sol, à savoir la teneur en eau, en gaz et la porosité. Ainsi, en fonction du type de sol, les flux de COV vers la surface vont différer. En effet, la diffusion d’une substance étant beaucoup plus élevée dans en phase gazeuse que dans l’eau (environ 4 ordres de grandeur), la proportion de ces fluides dans le milieu poreux va influer sur cette migration. Ainsi, en fonction des courbes capillaires du sol, le coefficient de diffusion effective sera modifié et les flux de contaminant vers la surface également. Pour calculer ce coefficient de diffusion effective, la formule à utiliser est celle proposée par Millington et Quirk (1961) :

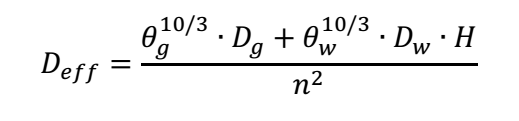
Avec :

• D_eff: le coefficient de diffusion effective (m² s⁻¹),
• D_g: le coefficent de diffusion du contaminant dans l’air (m² s⁻¹),
• D_w: le coefficent de diffusion du contaminant dans l’eau (m² s⁻¹),
• θ_g: la teneur en air (-),
• θ_w: la teneur en eau (-),
• H: la constante de Henry adimensionnelle (-, eau/gaz),
• n : la porosité totale du sol (-).

Par ailleurs, l’écoulement de la nappe va également avoir une influence sur ce coefficient de diffusion effective, puisqu’il va induire une « propagation » du contaminant dissous dans la nappe vers la frange capillaire par dispersion. Ainsi, l’équation du coefficient de diffusion effective s’écrit alors (Atteia et Höhener, 2010) :

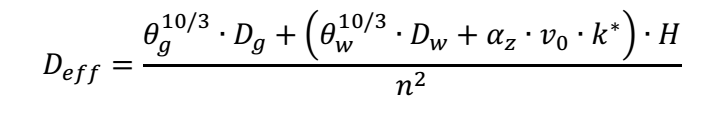
Avec :

• v₀: la vitesse d’écoulement de la nappe, ou vitesse de pore (m s⁻¹),
• α_z: la dispersivité (m),
• k* : le rapport de la conductivité hydraulique dans la frange capillaire sur la conductivité hydraulique à saturation (-).

Déterminer le profil de teneur en polluant avec l’Outil de calcul

Le tableur permet, à partir d’informations relatives au contaminant et aux propriétés hydrodynamiques du sol, de déterminer les flux de contaminant vers une surface libre et de réaliser la courbe de concentration pour le cas qui vous concerne. Les paramètres de van Genuchten étant difficile à déterminer, il peut être intéressant d’avoir une validation du profil de teneur en eau sur le site concerné.

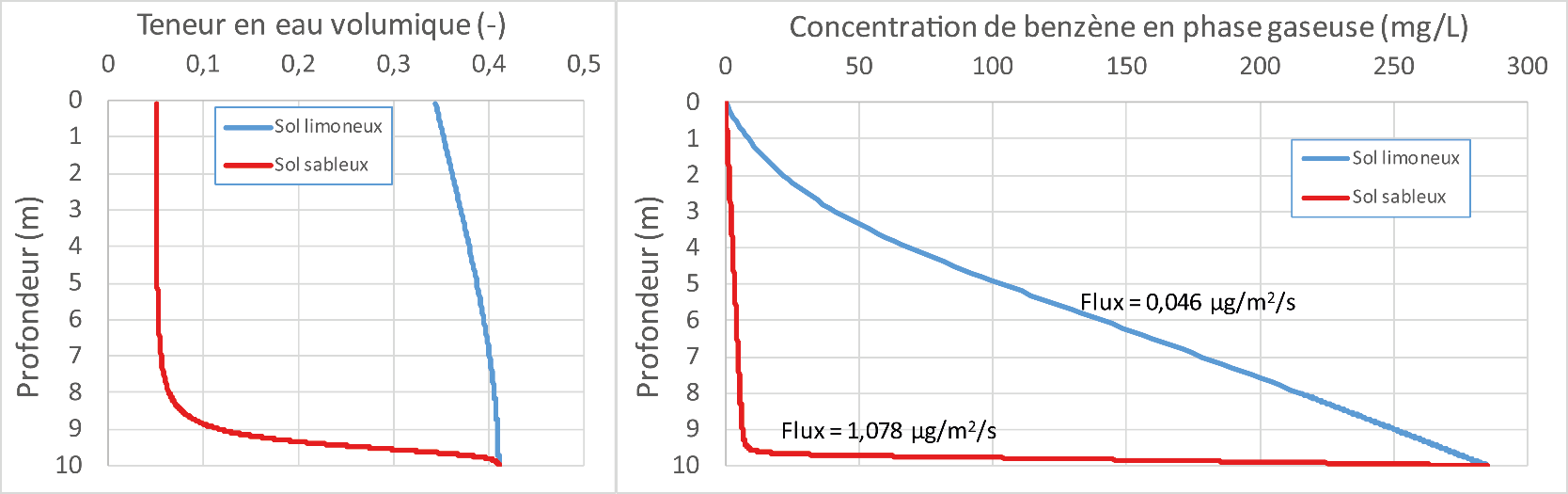
La Figure 3 illustre quelques résultats du modèle pour un sol sableux et un sol limoneux. Le point majeur est que la frange capillaire conduit à un gradient très élevé de concentration pour le cas du sol sableux, ce qui n’est pas le cas pour le sol limoneux. Ceci a été vérifié expérimentalement. En effet, la faible teneur en air pour le sol limoneux implique un déplacement très lent des composés et donc un coefficient de diffusion effective très faible induisant un flux de contaminant plus faible que pour le sol sableux. Il est donc courant d’avoir des concentrations dans l’eau du sol 100 à 1000 fois plus faibles au-dessus de la frange capillaire que dans la nappe dans le cas de franges capillaires de faible hauteur. Ainsi, il y a peu de cas où, en l’absence de contamination des sols, le flux de polluant émanant de la ZNS peut conduire à un risque élevé. Il est évident que ce modèle ne s’applique pas au cas où il y a une présence de phase flottante, qui conduit à des concentrations très élevées dans l’air du sol puisque, par définition, le produit flottant se situe dans la partie supérieure de la frange capillaire.

By G. Cohen, O. Atteia

Références

Atteia, O., Höhener, P., 2010. Semianalytical model predicting transfer of volatile pollutants from groundwater to the soil surface. Environ. Sci. Technol. 44, 6228–6232.

Fitzpatrick, N.A., Fitzgerald, J.J., 2002. An evaluation of vapor intrusion into buildings through a study of field data. Soil Sediment Contam. An Int. J. 11, 603–623.

Hers, I., Zapf-Gilje, R., Johnson, P.C., Li, L., 2003. Evaluation of the Johnson and Ettinger model for prediction of indoor air quality. Groundw. Monit. Remediat. 23, 119–133.

Millington, R.J., Quirk, J.P., 1961. Permeability of porous solids. Trans. Faraday Soc. 57, 1200–1207.

Van Genuchten, M.T., 1980. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils 1. Soil Sci. Soc. Am. J. 44, 892–898.